Porque colapsa un sistema de Colas

Teoría de colas

La teoría de colas es una disciplina, dentro de la investigación operativa, que tiene por objeto el estudio y análisis de situaciones en las que existen ente que demandan cierto servicio, de tal forma que dicho servicio no puede ser satisfecho instantáneamente, por lo cual se provocan esperas.          

Tal como queda patente en la definición anterior, el ámbito de la aplicación de la teoría de colas es enorme: desde las esperas para ser atendidos en establecimientos comerciales, esperas para ser procesados determinados programas informáticos, esperas para poder atravesar un cruce los vehículos que circulan por la ciudad esperas para establecer comunicación o recibir información de un sito web, a través de internet, entre muchas otras.     

Supuestos:

1) El sistema de cola existe siempre y cuando, el numero de entidades es mayor al numero de servidores.

2) La tasa de llegada (ʎ) y la tasa de servicio (µ) deben darse en proceso poissoniano, es decir las llegadas se da según la distribución poisson y el tiempo de servicios sigue una distribución exponencial.  

3) La tasa de servicio de un sistema debe ser menor que la tasa de llegada del mismo, de lo contrario el sistema colapsa. µ > ʎ

Sistemas de cola 

Los sistema están compuestos por un sistema de cola y un sistema de servicio, en el cual ingresan entes de una población mediante un proceso de llegada, para recibir un servicio requerido. El proceso de llegada puede ser medio por el tiempo entre llegada o por tasa de llegada, de igual forma el proceso de servicios puede ser medido por el tiempo entre servicios o la tasa de servicio

- Tasa de servicio µ: Numero de entidades promedio que pueden ser atendidas por el servidor en un lapso de tiempo.

- Tasa de llegada ʎ: Numero de entidades promedio que ingresan al sistema en un lapso de tiempo.

Diego Perez C.I 19.301.665

Teoria de Juegos

UNIVERSIDAD BICENTENARIA DE ARAGUA

FACULTAD DE INGENIERÍA

ESCUELA DE INGENIERÍA DE SISTEMAS

NUCLEO PUERTO ORDAZ

CATEDRA: SISTEMAS OPERATIVOS

	Teoría de Juegos

 

Profesora:                                                                             Bachilleres:

Ricardo Guevara                                                                    Diego Pérez C.I.19.301.665

                                                                                               Oswaldo Patriz  C.I. 20.885.097

Teoría de Juegos

La Teoría de Juegos consiste en la elaboración de recomendaciones sobre la forma razonable de las acciones de cada uno de los contrincantes en el curso de una situación de conflicto; es prácticamente una teoría matemática de las situaciones en conflicto. En un conflicto de juego los dos oponentes son llamados jugadores y cada uno de ellos tendrá un número finito o infinito de estrategias; a cada estrategia se encuentra asociada una recompensa que un jugador paga a otro.

La teoría de juegos es un área de la matemática aplicada que utiliza modelos para estudiar interacciones en estructuras formalizadas de incentivos (los llamados «juegos») y llevar a cabo procesos de decisión. Sus investigadores estudian las estrategias óptimas así como el comportamiento previsto y observado de individuos en juegos. Tipos de interacción aparentemente distintos pueden, en realidad, presentar estructura de incentivo similar y, por lo tanto, se puede representar mil veces conjuntamente un mismo juego.

Forma normal de un juego

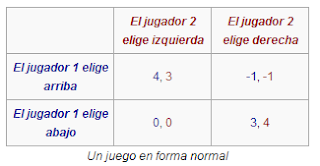
La forma normal (o forma estratégica) de un juego es una matriz de pagos, que muestra los jugadores, las estrategias, y las recompensas. Hay dos tipos de jugadores; uno elige la fila y otro la columna. Cada jugador tiene dos estrategias, que están especificadas por el número de filas y el número de columnas. Las recompensas se especifican en el interior. El primer número es la recompensa recibida por el jugador de las filas (el Jugador 1 en nuestro ejemplo); el segundo es la recompensa del jugador de las columnas (el Jugador 2 en nuestro ejemplo). Si el jugador 1 elige arriba y el jugador 2 elige izquierda entonces sus recompensas son 4 y 3, respectivamente.

Cuando un juego se presenta en forma normal, se presupone que todos los jugadores actúan simultáneamente o, al menos, sin saber la elección que toma el otro. Si los jugadores tienen alguna información acerca de las elecciones de otros jugadores el juego se presenta habitualmente en la forma extensiva.

También existe una forma normal reducida. Ésta combina estrategias asociadas con el

mismo pago.

Forma extensiva de un juego

La representación de juegos en forma extensiva modela juegos con algún orden que se debe considerar. Los juegos se presentan como árboles. Cada vértice o nodo representa un punto donde el jugador toma decisiones. El jugador se especifica por un número situado junto al vértice. Las líneas que parten del vértice representan acciones posibles para el jugador. Las recompensas se especifican en las hojas del árbol.

En el juego que se muestra en el ejemplo hay dos jugadores. El jugador 1 mueve primero y elige F o U. El jugador 2 ve el movimiento del jugador 1 y elige A o R. Si el jugador 1 elige U y entonces el jugador 2 elige A, entonces el jugador 1 obtiene 8 y el jugador 2 obtiene 2.

Los juegos en forma extensiva pueden modelar también juegos de movimientos simultáneos. En esos casos se dibuja una línea punteada o un círculo alrededor de dos vértices diferentes para representarlos como parte del mismo conjunto de información (por ejemplo, cuando los jugadores no saben en qué punto se encuentran).

La forma normal da al matemático una notación sencilla para el estudio de los problemas de equilibrio, porque desestima la cuestión de cómo las estrategias son calculadas o, en otras palabras, de cómo el juego es jugado en realidad. La notación conveniente para tratar estas cuestiones, más relevantes para la teoría combinatoria de juegos, es la forma extensiva del juego.

Juegos de Suma Cero

En los juegos de suma cero el beneficio total para todos los jugadores del juego, en cada combinación de estrategias, siempre suma cero (en otras palabras, un jugador se beneficia solamente a expensas de otros) el futbol, el ajedrez, el póker y el juego del oso son ejemplos de juegos de suma cero, porque se gana exactamente la cantidad que pierde el oponente. Como curiosidad, el fútbol dejó hace unos años de ser de suma cero, pues las victorias reportaban 2 puntos y el empate 1 (considérese que ambos equipos parten inicialmente con 1 punto), mientras que en la actualidad las victorias reportan 3 puntos y el empate 1.

                Se puede analizar más fácilmente un juego de suma cero, y cualquier juego se puede transformar en un juego de suma cero añadiendo un jugador "ficticio" adicional ("el tablero" o "la banca"), cuyas pérdidas compensen las ganancias netas de los jugadores.

La matriz de pagos de un juego es una forma conveniente de representación. Por ejemplo, un juego de suma cero de dos jugadores con la matriz que se muestra a continuación.

La matriz de recompensas de un juego es una forma de representación conveniente. Considérese el ejemplo del juego de suma cero mostrado a continuación:

	A	B	C
1	30, -30	-10, 10	20, -20
2	10, -10	20, -20	-20, 20
Un juego de suma cero

El orden de juego es el siguiente: el primer jugador elige en secreto una de las dos acciones 1 o 2; el segundo jugador; sin conocer la elección del primero, elige en secreto una de las tres acciones A, B o C. Entonces se revelan las elecciones de cada jugador y el total de puntos se ve afectado de acuerdo a la recompensa por tales elecciones.

Ejemplo: el primer jugador elige 2 y el segundo elige B. Cuando se asignan las recompensas, el primer jugador gana 20 puntos y el segundo pierde 20 puntos.

En este ejemplo los dos jugadores conocen la matriz de recompensas y tratan de maximizar sus puntos, ¿Qué deben hacer?

El jugador 1 puede razonar de la siguiente forma: "con la acción 2, puedo perder 20 puntos y ganar sólo 20, mientras que con la 1 puedo perder sólo 10 pero puedo ganar 30, así que 1 parece mucho mejor." Con un razonamiento similar, 2 elegirá C. Si los dos jugadores toman esas elecciones, el primer jugador ganará 20 puntos. ¿Pero qué pasa si el jugador 2 anticipa el razonamiento de 1, y elige B, para ganar 10 puntos? ¿o si el primer jugador anticipa este truco y elige 2, para ganar 20 puntos?

Para el ejemplo de arriba, resulta que el primer jugador debe de elegir 1 con probabilidad 57%, y la acción 2 con probabilidad 43%, mientras que el segundo debería asignar las probabilidades 0%, 57% y 43% a las tres opciones A, B y C.

El jugador 1 ganará entonces 2.85 puntos de media por juego.

Solución por Programación Lineal

Pasos del método de la programación lineal para determinar la estrategia aleatorizada Óptima.

1. Determine la matriz de recompensa R.

2. Si R tiene elementos no positivos, forme Rʼ  sumando una constante a cada elemento de R. Si E y Eʼ constituyen los valores esperados del juego asociados con las matrices de recompensa R y Rʼ, respectivamente, entonces Eʼ = E + (La Constante añadida).

3. Si el jugador renglón adopta una estrategia aleatorizada, donde las probabilidades de selecciones de los renglones 1 a n son P1 a Pnʼ respectivamente, entonces:

Pr = [ P1  P2 …. Pn ] donde P1 + P2 +…. + Pn = 1

Si el jugador columna adopta una estrategia pura, los valores esperados de dichas estrategias puras se incluyen en la matriz.

E (Pura)= Pr * Rʼ

Calcule E (Pura)

4. Resuelva P1 + P2 +…. + Pn = 1 para Pn = 1 y sustituya el resultado en E (Pura).

5. El valor esperado Eʼ  del juego es menor o igual que cada uno de los elementos de la matriz del paso 4. Cada una de esas desigualdades resultantes constituye una restricción en el problema de programación lineal. Liste estas restricciones.

6. Cada una de las probabilidades P1, P2, P3 , … debe ser menor o igual que 1. Liste estas restricciones.

7. Establezca el objetivo, que consiste en obtener el valor máximo de Z= Eʼ.

8. Resuelva el problema de programación lineal y determine los valores de P1  P2 …. Pn, y Eʼ.

9. Describa la estrategia aleatorizada óptima del jugador renglón proporcionando la probabilidad con la que el jugador debería elegir cada renglón.

10. Reste la constante del paso 2 de Eʼ para obtener E, el valor esperado del juego.

EJEMPLO: JUEGO DE DOS JUGADORES DE SUMA NULA

Aqui les dejo algunos links de como resolver ejercicios de Juegos de Suma Cero

http://www.youtube.com/watch?v=wixlx1R4IE8

http://www.youtube.com/watch?v=zFTS_ZOSnhU

Programación Dinamica

      Programación Dinámica

En muchos casos las decisiones del pasado afectan los escenarios del futuro. En estos casos se pueden tomar 2 opciones: asumir que el efecto temporal o dinámico es poco relevante y solo considerar modelos de un periodo (PPL) o considerar el efecto dinámico dentro del modelo (programación dinámica).

La programación dinámica nace después de la segunda guerra mundial, donde se presentó la necesidad de resolver procesos de decisión en múltiples etapas. Está técnica usa funciones recursivas y un principio de optimalidad, desarrollado por Bellman, para resolver este tipo de problemas.

El Modelo de Programación Dinámica

A continuación se muestra la formulación backward:

                     

     Describamos cada elemento:

1. Etapas: k

Particiones del problema en los cuales se pueden tomar decisiones que no dependan de estados anteriores, sino sólo del estado actual. Ej.: días, meses, años, etapas de producción en una línea, etc. Para su programación debe existir una etapa final (n).

2. Variables de Estado: Yk

Variables que caracterizan la situación en la que se encuentra el sistema en una etapa dada. Estás variables dan la independencia a la etapa actual de las etapas anteriores, por lo que deben  existir tantas variables de estado como las que permitan establecer en qué condiciones comienza (o finaliza) una etapa para su posterior optimización.

3. Variables de Decisión: Xk

Decisiones cuantificables cuyos valores se intenta determinar por medio de la resolución del modelo. Su valor determina el valor de las variables de estado de las etapas futuras.

4. Espacio de Soluciones Factibles: Ak(yk)

Espacio de soluciones factibles de las variables de decisión. Estos valores pueden depender de las variables de estado, es decir, para valores distintos de las variables de estado puede haber distintos espacios de soluciones factibles.

5. Ecuaciones de Recurrencia:

Función de Recursión: fk

Ecuación que indica cómo se acumula la función de valor desde la etapa k hasta la etapa final.

Función de Transformación: yk+1 = Tk(yk; xk)

Ecuación que indican como se relaciona las variables de estado y decisión de una etapa con la variable de estado de la etapa posterior.

6. Función de Valor o Beneficio: (Función Objetivo) Hk

Criterio de comparación entre distintos valores de las variables de estado. Es el objetivo a alcanzar por la resolución del problema en cada etapa.

7. Condiciones de Borde: y1 = M y fn+1(yn+1) = F

Limitaciones que deben imponerse al problema, corresponden a condiciones iniciales o finales que deben cumplirse.

       Veamos algunas características de este modelo importantes de ser destacadas

1. Esta formulación tiene el concepto de recursividad, que es la generalización del concepto dinámico del modelo. Esto se observa en que fk(yk) es definido en función de las variables (yk, xk) del periodo k y en función de sí misma en el periodo siguiente (fk+1(yk+1)).

2. Las condiciones de borde permiten obtener la solución explícita del modelo, ya que la etapa n requiere conocer fn+1, y la etapa 1 requiere desparametrizar la solución, asignando un valor conocido a y1.

3. La función Hk corresponde a la representación de la función.0 objetivo en la etapa k hasta la etapa n. Ella debería construirse de manera de ir dando cuenta del valor de la función objetivo en cada etapa.

4. La función de transformación Tk(yk; xk) establece la relación entre las variables de Estado yk e yk+1 para 2 periodos consecutivos. La variable de estado de la etapa siguiente (yk+1) es expresada como una función de la variable de estado (yk) y de la variable de decisión (xk) de la etapa actual.

5. El conjunto Ak representa al conjunto de restricciones asociadas a la variable de decisión de la etapa k. Estas restricciones sólo deben incluir a las variables de decisión de la etapa k y no deben incluir a las de otras etapas.

6. La solución del subproblema de optimización en la etapa k, es una solución Paramétrica en la variable de estado yk, ya que f es en función de ella. Este subproblema de optimización tiene como variable de decisión a xk, y el resultado es leído como: “para la etapa k, xk es la mejor decisión para un yk dado, y fk(yk) es el mejor valor de la función objetivo desde la etapa k hasta la etapa n”.

7. Se denomina política ´optima de la etapa k; k + 1; … ; n para un determinado estado inicial en la etapa k. La política ´optima global, esto es, desde la etapa 1, constituye la solución ´optima del problema, puesto que en la etapa 1 se tiene sólo un estado inicial factible.

      ECUCACION RECURSIVA DE RETROCESO

La diferencia principal entre los métodos de avance y de retroceso ocurre en la forma como definimos el estado del sistema.

Este método de cálculo se conoce como procedimiento de avance porque los cálculos avanzan de la primera hasta la última etapa. Sin embargo, cuando el lector estudie la mayoría de las obras dedicadas a la programación dinámica, advertirá que la ecuación recursiva se construye de manera que los cálculos comienzan en la última etapa y después “regresan” hacia la etapa 1. Este método recibe el nombre de procedimiento de retroceso.

Los cálculos se efectúan en el orden

Este método de cálculo de conoce como procedimiento de avance porque los cálculos avanzan de la primera a la última etapa. Sin embargo, cuando el lector estudie la mayoría de las obras dedicadas a la programación dinámica advertirá que la ecuación recursiva se construye de manera que los cálculos comienzan en la última etapa y después “regresan” hacia la etapa 1. Este método recibe el nombre de 

Procedimiento de retroceso

La diferencia principal entre los métodos de avance y de retroceso ocurre en la forma en que definimos el estado del sistema. Para ser específicos, volveremos a considerar el ejemplo del presupuesto de capital. Para el procedimiento de retroceso, definimos los estados yj como:

y1 = monto de capital asignado a las etapas 1, 2 y 3
y2 = monto de capital asignado a las etapas 2 y 3
y3 = monto de capital asignado a la etapa 3

Para apreciar la diferencia entre la definición de los estados xj y yj en los métodos de avance y retroceso, las dos definiciones se resumen en forma gráfica La ecuación recursiva de retroceso se escribe, por tanto como:

Texto utilizado para la investigación:

http://www.eumed.net/libros-gratis/2006c/216/1j.htm

http://www.slideshare.net/Alexdfar/programacin-dinmica-5688350

http://www.slideshare.net/elmergabrielchanpech/programacin-dinmica-15433493

http://cms.dm.uba.ar/materias/1ercuat2009/optimizacion/Maurette_Ojea.pdf

BACHILLERES:

Jesús Colmenares

Rodolfo Cabeza

Angel Espinoza   

Procesos Estocasticos

Universidad Bicentenaria de Aragua

Cátedra: Investigación de Operaciones II

Escuela de Ingeniería en Sistemas

Cadenas de Markov

               Una cadena de Markov es una sucesión de ensayos similares u observaciones en la cual cada ensayo tiene el mismo número finito de resultados posibles y en donde la probabilidad de cada resultado para un ensayo dado depende sólo del resultado del ensayo inmediatamente precedente y no de cualquier resultado previo

Propiedad de Markov

         Dada una secuencia de variables aleatorias X1, X2 ,X3, tales que el valor   de  xn es el estado del proceso en el tiempo n. Si la  distribución de probabilidad condicional de Xn+1 en estados pasados es una función de Xn por sí sola, entonces:

P ( X+1= xn+1 /Xn= xn , Xn-1= xn-1 ,....X2= x2 , X1= x1)=

P (Xn+= xn+1 /Xn= xn )

Donde xi es el estado del proceso en el instante i.

Esta identidad es la denominada propiedad de Markov:  El estado en t + 1 sólo depende del estado en t  y no de la evolución anterior del sistema.

Matriz de transición

             Al trabajar con cadenas de Markov, a menudo es útil pensar la sucesión de ensayos como experimentos efectuados en cierto sistema físico, cada resultado dejando a este sistema en cierto estado.

             Por ejemplo, consideremos una sucesión de elecciones políticas en cierto país: el sistema podría tomarse como el país mismo y cada elección lo dejaría en cierto estado, es decir en el control del partido ganador. Si sólo hay dos partidos políticos fuertes, llamados A y B, los que por lo regular controlan el gobierno, entonces podemos decir que el país se encuentra en el estado A o B si el partido A o B ganara la elección. Cada ensayo (o sea cada elección), coloca al país en uno de los dos estados A o B. Una  sucesión de 10 elecciones podría producir resultados tales como los siguientes:

A, B, A, A, B, B, B, A, B, B

               La primera elección en la sucesión deja en el poder al partido A, la segunda fue ganada por el partido B, y así sucesivamente, hasta que la décima elección la gane el partido B. Supongamos que las probabilidades de que el partido A o B ganen la próxima elección son determinadas por completo por el partido que está en el poder ahora. Por ejemplo podríamos tener las probabilidades siguientes:

     

• Si el partido A está en el poder, existe una probabilidad de ¼ que el partido A ganará la próxima elección y una probabilidad de ¾ de que el partido B gane la elección siguiente.

• Si el partido B está en el poder, hay una probabilidad de 1/3 de que el partido A gane la elección siguiente y una probabilidad de 2/3 que el partido B permanezca en el poder.

 

 Definición: Consideremos un proceso de Markov en que el sistema posee n estados posibles, dados por los números 1, 2, 3, …., n. Denotemos pij  a la probabilidad de que el sistema pase al estado j después de cualquier ensayo en donde su estado era i antes del ensayo. Los números pij se denominan probabilidades de transición y la matriz nxn P = (pij ) se conoce como matriz de transición del sistema.

Observaciones: 

1) La suma pi1+pi2+......+pin=1 Esta suma representa la probabilidad de que el sistema pase a uno de los estados 1, 2, …., n dado que empieza en el estado i. Ya que el sistema ha de estar en uno de estos n estados, la suma de probabilidades debe ser igual a 1. Esto significa que los elementos en cualquier renglón de la matriz de transición deben sumar 1.

2) Cada elemento pij> o igual a 0.

 

Procesos Estocásticos

       Se define entonces una familia de variables aleatorias que dependen de una variable determinista, (en este caso el tiempo). Se define el proceso estocástico X(t) como el número de llamadas que se producen en la centralita en el tiempo (0,t). Así, para cada valor de t que se elija, tendremos una variable aleatoria distinta, con forma similar pero distinto valor. En los temas anteriores definimos X(x), en este caso X(λ). Ahora debemos x t) este caso λ t)  representar X(x,t), en este caso, X(λ,t). En general, diremos X(t) igual que antes llamábamos X y no X(λ).

Proceso Estocástico

Es una función de dos variables, t y x, una determinista y otra aleatoria

a) X(x,t) es una familia de funciones temporales.

b) Si se fija x, tenemos una función temporal X(t) llamada realización del proceso.

c) Si se fija t, tenemos una Variable Aleatoria.

d) Si se fijan t y x, tenemos un número real o complejo (muy normal en teoría de la señal).

Los procesos estocásticos pueden ser clasificados en:

- Tiempo discreto: Cuando el valor de la variable sólo puede cambiar en  una serie de momentos determinados del tiempo (por ejemplo, los sorteos de la lotería tienen lugar en determinadas fechas).

- Tiempo continuo: Cuando el valor de la variable puede cambiar en cualquier momento del tiempo (la temperatura, por ejemplo).

 Otra forma de clasificar a los procesos estocásticos es:

- Variable continua: La variable puede tomar cualquier valor comprendido en un rango (la temperatura, por ejemplo) 

 

- Variable discreta: La variable sólo puede tomar determinados valores o estados discretos.

Características de un proceso estocástico

       Del mismo modo que en una variable unidimensional X, podemos calcular su media, su varianza y otras características, y en variables n-dimensionales obtenemos un vector de medias, matriz de covarianzas, etc., en un proceso estocástico podemos obtener algunas características que describen su comportamiento: medias, varianzas y covarianzas. Puesto que las características del proceso pueden variar a lo largo de t estas características no serán parámetros sino que serán funciones de t.

Media : Llamaremos función de medias del proceso a una función de t que proporciona las medias de las distribuciones marginales para cada instante t.

E [ x(t) ] = µ_t

Varianza : Llamaremos función de varianzas del proceso a una función de t que proporciona las varianzas de las distribuciones marginales para cada instante t.

Var [ x(t) ] = σ2(t) = E [ (x(t) - µ_t)2 ]

Autovarianzas : Llamaremos función de autocovarianzas del proceso a la función que proporciona la covarianza existente entre dos instante de tiempo cuales quiera.

Cov(t₁, t₂)=E[(x(t₁)-µ_t1)(x(t₂)-µ_t2)]

Autorrelacion : Llamaremos función de autocorrelación a la estandarización de la función de

Covarianzas.

ρ(t₁, t₂) = Cov (t₁, t₂) / σ(t₁) σ(t₂)

Matriz ergodica

       Una cadena de markov es ergodica (se conoce cm una cadena markov a un tipo especial de proceso estocástico discreto en el que la probabilidad de que ocurra un evento depende del evento inmediatamente anterior. En efecto, las cadenas de este tipo tienen memoria). Si todos sus estados son no nulos, no periódicos y recurrentes.

Estado de absorción

      Un estado absorbente en un sistema de markov es un estado a partir de la cual existe cero probabilidades de salir. Un sistema absorbente de markov es un sistema de markov que contiene al menos un estado absorbente, tal que es posible llegar a un estado absorbente  después de algún numero de etapas comenzando en cualquier estado no absorbente.

En el análisis de los sistemas absorbentes, enumeramos los estados en tal manera que los estados absorbentes  son los últimos.

      Aquí I esta la matriz unidad m×m(m=numero de estados absorbentes), S es una matriz cuadrada (n-m)×(n-m) (n=número total de estados, de modo n-m=el numero de estados absorbentes), 0 es una matriz ceros y T es una matriz (n-m)×m.

La matriz S es la matriz de transacción para la circulación entre los estados de absorción. 

 Bachilleres:

Martinez Elys 

Mata Crisbel

Ruiz Solmaira

Escuela de Ingeniería en Sistemas